This article has two goals. The first one is to show how two PyTorch convolutions can be combined into one. If you want the realisation, scroll through the article to the end.
The second, the main goal is to take a closer look into the convolution realisation by the convolution merge example. We will learn how they are stored and used particularly in PyTorch without hardcore details like im2col. Before we start looking at the implementation, let’s remember what we are working with.
Let’s start with the terminology. A neural network, or computational graph, is a set of operations (layers) that are applied to the input object or to the outputs of other operations. We are interested in computer vision and convolutions, so the input object will be a picture: a tensor of size [number of channels X height X width], where the number of channels is most often 3 (RGB). Intermediate outputs will be called a feature map. A feature map is in some sense the same picture, only the number of channels is arbitrary, and each cell of the tensor is called a feature, not a pixel. And in order to be able to run several images at once in one pass, all these tensors have an additional dimension of the size equal to the number of objects in the batch (one run).
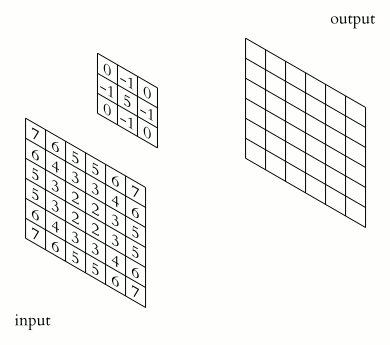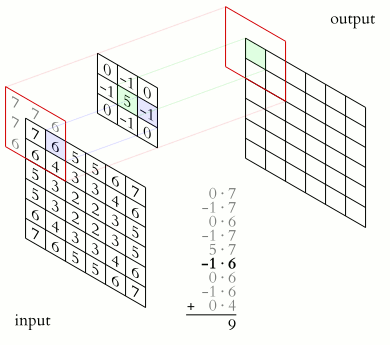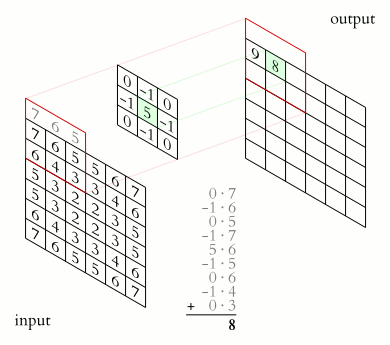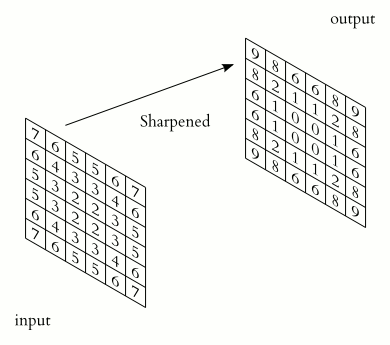
Now let’s move on to cross-correlation. It is often confused with convolution, but for our purposes, these two operations must be distinguished. What is cross-correlation in the context of neural networks? First of all, cross-correlation has a kernel. The kernel is a tensor with shape [number of channels X kernel height X kernel width]. And the cross-correlation operation can be represented as sliding off the kernel along the input feature map as on a gif. Each time we apply a kernel to a piece of input, we multiply the corresponding kernel weights with the features and add them up, getting a new feature in the output channel.
It’s time to tell you what a convolution is. Convolution is almost a cross-correlation, only the kernel is reflected relative to the horizontal and vertical axes. This difference is often omitted because it is not important for understanding the neural networks, but this time the difference is important since we will work with weights directly.
You probably noticed that the convolution described above creates one channel from a set. In neural networks, convolutions create another set from a set of channels. This is achieved by the fact that several kernels described above are stored in the convolution layer at once, each of which generates one channel, and then they are concatenated. The final dimension of the kernel of such a convolution is: [number of channels per output X number of channels per input X core height X core width]
The next part of the convolution layer in PyTorch and in many other frameworks is bias. Bias is an addition to each output channel. So, bias is a set of parameters, with a size equal to the number of output channels.
It’s time to remember our task. The task is to combine two convolutions into one. Why is this even possible? The short answer is that convolution and bias addition are linear operations. And the combination of linear operations is a linear operation. If this explanation is not clear enough, don’t be upset. The following examples will prove the statement on practice.
Let’s start with the simplest case. One convolution of arbitrary size, the second 1x1. None of them has bias. Both make one channel from one channel. The convolution of 1x1 makes this case even more simple. In fact, it means multiplying the feature map by a constant. So, you can simply multiply the weights of the first convolution by this very constant.
import torch
import numpy as np
conv1 = torch.nn.Conv2d(1, 1, (3, 3), bias=False) # [каналы на вход X на выход X размер ядра]
conv2 = torch.nn.Conv2d(1, 1, (1, 1), bias=False) # свёртка 1х1. Если посмотреть на ее веса, там будет ровно одно число.
new_conv = torch.nn.Conv2d(1, 1, 3, bias=False) # Вот эта свёртка объеденит две.
new_conv.weight.data = conv1.weight.data * conv2.weight.data
# проверим что все сработало
x = torch.randn([1, 1, 6, 6]) # [Размер батча X кол-во каналов X размер по вертикали X размер по горизонтали]
out = conv2(conv1(x))
new_out = new_conv(x)
assert (torch.abs(out - new_out) < 1e-6).min()
Let’s make it more interesting. Now let the first convolution transform an arbitrary number of channels into another arbitrary number. In this case, our 1x1 convolution will be the weighted sum of the intermediate feature map channels. And this means that you can make a weighted sum of the weights that generate these channels.
conv1 = torch.nn.Conv2d(2, 3, (3, 3), bias=False) # [каналы на вход X на выход X размер ядра]
conv2 = torch.nn.Conv2d(3, 1, (1, 1), bias=False) # свёртка 1х1. Если посмотреть на ее веса, то уже будет 3 числа.
new_conv = torch.nn.Conv2d(2, 1, 3, bias=False) # В итоге мы хотим из двух каналов получить 1.
# Веса свёртки — тензор размера: [каналы на выход X каналы на вход X размер ядра1 X размер ядра2]
# Чтобы домножить по первому измерению веса, отвечающие за создание каждого промежуточного канала с их весом,
# нам придется пермьютнуть размерности второй второй свертки.
# Затем суммируем взвешенные веса и дорисовываем измерение, дабы успешно подменить веса.
new_conv.weight.data = (conv1.weight.data * conv2.weight.data.permute(1, 0, 2, 3)).sum(0)[None, ]
x = torch.randn([1, 2, 6, 6])
out = conv2(conv1(x))
new_out = new_conv(x)
assert (torch.abs(out - new_out) < 1e-6).min()
Let’s make it even more interesting. Now let both of our convolutions transform an arbitrary number of channels into another arbitrary number. In this case, our 1x1 convolution will be a set of weighted sums of the intermediate feature map channels. The logic is the same here. It is necessary to sum up the weights generating the intermediate features with the weights from the second convolution.
conv1 = torch.nn.Conv2d(2, 3, 3, bias=False)
conv2 = torch.nn.Conv2d(3, 5, 1, bias=False)
new_conv = torch.nn.Conv2d(1, 5, 3, bias=False) # Забавный факт:
# Не важно какие размеры передавать при инициализации.
# Подмена весов все исправит.
# Магия бродкаста в действии. Можно было сделать так и в предыдущем примере, но что-то же должно улучшаться.
new_conv.weight.data = (conv2.weight.data[..., None] * conv1.weight.data[None]).sum(1)
x = torch.randn([1, 2, 6, 6])
out = conv2(conv1(x))
new_out = new_conv(x)
assert (torch.abs(out - new_out) < 1e-6).min()
Now, it’s time to abandon the limit on the size of the second convolution. To simplify, let’s look at a one-dimensional convolution. What will operation ‘k’ look like with kernel 2? $$k_1 * x_1 + k_2 * x_2$$ Let’s add additional convolution ‘v’ with kernel size 2: $$v_1 * (k_1 * x_i + k_2 * x_{i+1}) + v_2 * (k_1 * x_{i+1} + k_2 * x_{i+2})$$ Reformating the equation: $$x_i * v_1 * k_1 + x_{i+1} * (v_1 * k_2 + v_2 * k_1) + x_{i+1} * (k_2 * v_2)$$ And finally, let’s add some zeros. $$x_i * (v_1 * k_1 + 0 * v_2)+ x_{i+1} * (v_1 * k_2 + v_2 * k_1) + x_{i+1} * (0 * v_1 + k_2 * v_2)$$ What did we get? The result is a convolution with kernel 3. And the kernel in this convolution is a result of cross-correlation applied to padded weights of the first convolution with a kernel created by weights of the second convolution.
For other sizes of kernels, for the two-dimensional case, and the multichannel case, the same logic works. But I will not provide math for these complex cases, instead, I will show you how to transform this idea into code.
kernel_size_1 = np.array([3, 3])
kernel_size_2 = np.array([3, 5])
kernel_size_merged = kernel_size_1 + kernel_size_2 - 1
conv1 = torch.nn.Conv2d(2, 3, kernel_size_1, bias=False)
conv2 = torch.nn.Conv2d(3, 5, kernel_size_2, bias=False)
new_conv = torch.nn.Conv2d(2, 5, kernel_size_merged, bias=False)
# Считаем сколько нулей надо дорисовать вокруг первой свёртки
# Паддинг это сколько нулей надо нарисовать вокруг входной фичимапы по вертикали и горизонтали
padding = [kernel_size_2[0]-1, kernel_size_2[1]-1]
new_conv.weight.data = torch.conv2d(conv1.weight.data.permute(1, 0, 2, 3), # Уже знакомый нам трюк. Мотивация та же.
conv2.weight.data.flip(-1, -2), # А вот это нужно чтобы свертку преваритить в кросс-корреляцию.
padding=padding).permute(1, 0, 2, 3)
x = torch.randn([1, 2, 9, 9])
out = conv2(conv1(x))
new_out = new_conv(x)
assert (torch.abs(out - new_out) < 1e-6).min()
Now let’s add biases. We will start with a bias in the second convolution. Let me remind you that bias is a vector the size of the number of output channels, which is then added to the output of the convolution. Well, that means we just need to put the bias of the second convolution in the result one.
kernel_size_1 = np.array([3, 3])
kernel_size_2 = np.array([3, 5])
kernel_size_merged = kernel_size_1 + kernel_size_2 - 1
conv1 = torch.nn.Conv2d(2, 3, kernel_size_1, bias=False)
conv2 = torch.nn.Conv2d(3, 5, kernel_size_2, bias=True)
x = torch.randn([1, 2, 9, 9])
out = conv2(conv1(x))
new_conv = torch.nn.Conv2d(2, 5, kernel_size_merged, bias=True)
padding = [kernel_size_2[0]-1, kernel_size_2[1]-1]
new_conv.weight.data = torch.conv2d(conv1.weight.data.permute(1, 0, 2, 3),
conv2.weight.data.flip(-1, -2),
padding=padding).permute(1, 0, 2, 3)
new_conv.bias.data = conv2.bias.data # вот тут интересность
new_out = new_conv(x)
assert (torch.abs(out - new_out) < 1e-6).min()
Adding a bias to the first convolution is a little more complicated. Therefore, we will go in two stages. To begin with, we note that the use of bias in convolution is equivalent to creating an additional feature map in which the features of each channel will be constants and equal to the bias parameters. Then add this feature to the output of the convolution.
kernel_size_1 = np.array([3, 3])
kernel_size_2 = np.array([3, 5])
kernel_size_merged = kernel_size_1 + kernel_size_2 - 1
conv1 = torch.nn.Conv2d(2, 3, kernel_size_1, bias=True)
conv2 = torch.nn.Conv2d(3, 5, kernel_size_2, bias=False)
x = torch.randn([1, 2, 9, 9])
out = conv2(conv1(x))
new_conv = torch.nn.Conv2d(2, 5, kernel_size_merged, bias=False)
padding = [kernel_size_2[0]-1, kernel_size_2[1]-1]
new_conv.weight.data = torch.conv2d(conv1.weight.data.permute(1, 0, 2, 3),
conv2.weight.data.flip(-1, -2),
padding=padding).permute(1, 0, 2, 3)
new_out = new_conv(x)
add_x = torch.ones(1, 3, 7, 7) * conv1.bias.data[None, :, None, None] # Тут делается доп фичимапа
new_out += conv2(add_x)
assert (torch.abs(out - new_out) < 1e-6).min()
But we don’t want to create this extra feature every time, we want to somehow change the convolution parameters. And we can do it. It is enough just to note that after applying convolution over a constant feature map, another constant feature map will be obtained. The motivation is simple — wherever we put the window, the slice will be the same. So, it’s enough for us to convolve this feature map just once, see what features we get on each channel, and put them in bias.
kernel_size_1 = np.array([3, 3])
kernel_size_2 = np.array([3, 5])
kernel_size_merged = kernel_size_1 + kernel_size_2 - 1
conv1 = torch.nn.Conv2d(2, 3, kernel_size_1, bias=True)
conv2 = torch.nn.Conv2d(3, 5, kernel_size_2, bias=True)
x = torch.randn([1, 2, 9, 9])
out = conv2(conv1(x))
new_conv = torch.nn.Conv2d(2, 5, kernel_size_merged)
padding = [kernel_size_2[0]-1, kernel_size_2[1]-1]
new_conv.weight.data = torch.conv2d(conv1.weight.data.permute(1, 0, 2, 3),
conv2.weight.data.flip(-1, -2),
padding=padding).permute(1, 0, 2, 3)
add_x = torch.ones(1, 3, *kernel_size_2) * conv1.bias.data[None, :, None, None]
# Эта операция одновременно переносит биас из первой свертки и добавляет биас второй.
new_conv.bias.data = conv2(add_x).flatten()
new_out = new_conv(x)
assert (torch.abs(out - new_out) < 1e-6).min()
It remains just to wrap it all in a function, removing the magic constants for dimensions.
import torch
import numpy as np
def merge_two_conv(conv1, conv2):
kernel_size_1 = np.array(conv1.weight.size()[-2:])
kernel_size_2 = np.array(conv2.weight.size()[-2:])
kernel_size_merged = kernel_size_1 + kernel_size_2 - 1
in_channels = conv1.weight.size()[1]
out_channels = conv2.weight.size()[0]
inner_channels = conv1.weight.size()[0]
new_conv = torch.nn.Conv2d(in_channels, out_channels, kernel_size_merged)
padding = [kernel_size_2[0]-1, kernel_size_2[1]-1]
new_conv.weight.data = torch.conv2d(conv1.weight.data.permute(1, 0, 2, 3),
conv2.weight.data.flip(-1, -2),
padding=padding).permute(1, 0, 2, 3)
add_x = torch.ones(1, inner_channels, *kernel_size_2)
add_x *= conv1.bias.data[None, :, None, None]
new_conv.bias.data = torch.conv2d(add_x,
conv2.weight.data).flatten()
new_conv.bias.data += conv2.bias.data
return new_conv
conv1 = torch.nn.Conv2d(2, 3, 3)
conv2 = torch.nn.Conv2d(3, 5, (4, 5))
new_conv = merge_two_conv(conv1, conv2)
x = torch.randn([1, 2, 9, 9])
assert (torch.abs(conv2(conv1(x)) - new_conv(x)) < 1e-6).min()
At the end of the article, I want to say that our function will not work with every convolution. In this implementation, we did not take into account padding, dilation, strides, or groups. But nevertheless, I showed everything I wanted. It probably makes little sense to improve it further, since I have seen the tasks of collapsing two convolutions into one only once, (here), and even here, the second convolution was 1x1.